Soit N échantillons d'une courbe d'abscisses
x1, x2, ..., xn et d'ordonnées y1, y2, …, yn. Nous
allons chercher l'équation P(x)=a0+a1x de la droite qui se
rapproche au mieux de ces points au sens des moindres carrés. Le
principe est de minimiser la somme des carrés des différences
entre les points réels et les points interpolés :
En développant cette expression nous avons :
Les valeurs de a0 et a1 sont
telles
que les dérivées partielles de S sont nulles :
et 
Soit :
Et :
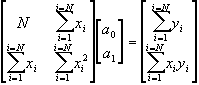
En résolvant ce système, nous obtenons :
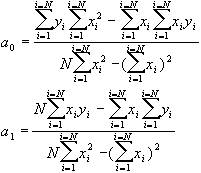
Cette méthode se généralise
à un polynôme de degré quelconque mais aussi à
un polynôme ayant un nombre de variables quelconque. Comme nous
travaillons
sur des images, nos polynômes auront deux variables x et y
décrivant la position des pixels dans l'image. Reprenons les calculs
pour un polynôme de deux variables et de degré deux. Le polynôme
aura la forme suivante :
Le système à résoudre est finalement le suivant
:
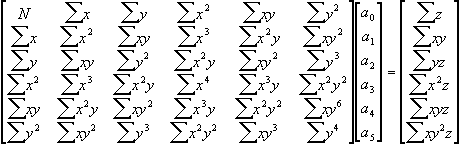
Attention dans ce système tous les 
ont
été écrits 
et
toutes les variables x et y sont en fait indicées.
Pour trouver les coefficients du polynôme il suffit alors de résoudre
ce système par une méthode de Gauss classique.
Voyons comment cela se traduit en Pascal. Nous commençons par initialiser les variables :
degre:=2;Degré contient le degré du polynôme. Dim contient les dimensions de la matrice principale du système.
dim=6;
Puis nous calculons les différentes sommes :
sx1:=0; sy1:=0; sz:=0;n contient le nombre de points. xi, yi, zi sont des tableaux qui contiennent les points choisis dans l'image. Toutes les variables commençant par s comme " somme " servent à calculer les différentes sommes qui deviendront coefficients de la matrice principale. On complète les coefficients de la matrice principale et du second terme :
sx2:=0; sy2:=0; sxy:=0;
sxz:=0; syz:=0;
sx3:=0; sy3:=0; sx2y:=0;
sxy2:=0; sx4:=0; sy4:=0;
sx3y:=0; sx2y2:=0; sxy3:=0;
sxyz:=0; sx2z:=0; sy2z:=0;for j:=1 to n do
begin
sx1:=sx1+xi[j];
sy1:=sy1+yi[j];
sz:=sz+zi[j];
sx2:=sx2+xi[j]*xi[j];
sy2:=sy2+yi[j]*yi[j];
sxy:=sxy+xi[j]*yi[j];
sxz:=sxz+xi[j]*zi[j];
syz:=syz+yi[j]*zi[j];
sx3:=sx3+xi[j]*xi[j]*xi[j];
sy3:=sy3+yi[j]*yi[j]*yi[j];
sxyz:=sxyz+xi[j]*yi[j]*zi[j];
sx2z:=sx2z+xi[j]*xi[j]*zi[j];
sy2z:=sy2z+yi[j]*yi[j]*zi[j];
sx2y:=sx2y+xi[j]*xi[j]*yi[j];
sxy2:=sxy2+xi[j]*yi[j]*yi[j];
sx4:=sx4+xi[j]*xi[j]*xi[j]*xi[j];
sy4:=sy4+yi[j]*yi[j]*yi[j]*yi[j];
sx3y:=sx3y+xi[j]*xi[j]*xi[j]*yi[j];
sx2y2:=sx2y2+xi[j]*xi[j]*yi[j]*yi[j];
sxy3:=sxy3+xi[j]*yi[j]*yi[j]*yi[j];
end;
a[1,1]:=n; a[1,2]:=sx1; a[1,3]:=sy1; a[1,4]:=sxy; a[1,5]:=sx2; a[1,6]:=sy2;a contient la matrice principale. yg contient les coefficients du second terme à droite du = dans l'équation. On peut alors résoudre le système par la méthode de Gauss que l'on trouve dans tous les livres de base :
a[2,1]:=sx1; a[2,2]:=sx2; a[2,3]:=sxy; a[2,4]:=sx2y; a[2,5]:=sx3; a[2,6]:=sxy2;
a[3,1]:=sy1; a[3,2]:=sxy; a[3,3]:=sy2; a[3,4]:=sxy2; a[3,5]:=sx2y; a[3,6]:=sy3;
a[4,1]:=sxy; a[4,2]:=sx2y; a[4,3]:=sxy2; a[4,4]:=sx2y2; a[4,5]:=sx3y; a[4,6]:=sxy3;
a[5,1]:=sx2; a[5,2]:=sx3; a[5,3]:=sx2y; a[5,4]:=sx3y; a[5,5]:=sx4; a[5,6]:=sx2y2;
a[6,1]:=sy2; a[6,2]:=sxy2; a[6,3]:=sy3; a[6,4]:=sxy3; a[6,5]:=sx2y2; a[6,6]:=sy4;
yg[1]:=sz; yg[2]:=sxz; yg[3]:=syz; yg[4]:=sxyz; yg[5]:=sx2z; yg[6]:=sy2z;
for k:=1 to dim-1 doxg contient alors les coefficients a0 à a5 du polynôme après les calculs. On synthétise finalement la nouvelle image :
begin
dp:=1/a[k,k];
for j:=k to dim do a[k,j]:=a[k,j]*dp;
yg[k]:=yg[k]*dp;
for j:=k+1 to dim do
begin
d:=a[j,k];
for l:=k to dim do a[j,l]:=a[j,l]-d*a[k,l];
yg[j]:=yg[j]-d*yg[k];
end;
end;xg[dim]:=yg[dim]/a[dim,dim];
for i:=1 to dim-1 do
begin
s:=0;
for j:=dim-i+1 to nl do s:=s+a[dim-i,j]*xg[j];
xg[dim-i]:=yg[dim-i]-s;
end;
for j:=1 to sy doLa nouvelle image synthétisée est placée ici dans le tableau image de largeur sx et de hauteur sy. Voici la procédure que vous pouvez télécharger ici : Synthèse degré 2.zip (1K). Avec cette procédure, vous disposez de tout le matériel nécessaire à la réalisation d'une fonction permettant d'effacer certains détails d'une image ( fonctions WIPE de Qmips et BOUCHER UNE ZONE de Prism ).
begin
for i:=1 to sx do
begin
val:=xg[1]+xg[2]*i+xg[3]*j+xg[4]*i*j+xg[5]*i*i+xg[6]*j*j;
image[i,j]:=round(val);
end;
end;