![]()
Dans cet article, je vais tenter de prouver par l'exemple la
supériorité
de la méthode par Superstar utilisée par les professionnels
sur la méthode classique de photométrie différentielle.
Les flux seront mesurés par la fonction de modélisation
Gaussienne de Prism.
Pour les lecteurs peu familiers de ces deux méthodes, je commencerais par une présentation de celles ci.
1 ) La méthode classique
La méthode classique de photométrie différentielle est une application directe de la loi de Pogson qui donne la relation liant la différence de magnitude de deux étoiles à leurs flux :
M2 - M1 = - 2,5 . log ( F2 / F1 )
Soit :
M2 = M1 - 2,5 . log ( F2 / F1 )
Par conséquent, si l'on connaît la magnitude M1 d'une étoile étalon trouvée dans un catalogue on peut facilement en déduire la magnitude M2 d'une étoile proche . Il suffit de prendre une photo des deux étoiles pour en mesurer les flux F1 et F2. Connaissant F1, F2 et M1, il est alors facile de calculer M2.
3 ) La méthode de la Superstar
Il est possible d'améliorer la précision de la mesure en utilisant une étoile étalon plus brillante si l'on considère que le bruit sera proportionnellement plus faible. Le rapport signal/bruit de la mesure sera alors plus élevé et la mesure plus précise. Donc, si on a le choix, il vaut mieux prendre l'étalon le plus brillant.
En étendant ce principe, il est même possible de créer un étalon imaginaire trés brillant à partir de plusieurs étoiles de l'image. Il suffit d'ajouter les flux de celles ci. On crée alors une "super étoile" ou "Superstar" donnant le nom de cette méthode.
Dans cette méthode, on utilise toujours la loi de Pogson :
M2 = Met -2,5.log ( F2 / Fet )
Mais ici, le flux de l'étalon F1 est remplacé par le flux total de tous les étalons Fet. La magnitude de l'étalon M1 est aussi remplacée par par la magnitude théorique Met de la Superstar.
Le calcul de cette magnitude mérite quelques expliquations.
Les Magnitudes Me1,Me2,......,Men sont données
par les catalogues.
On attribut arbitrairement à l'étalon 1 un flux de valeur
1. Cela ne change rien aux calculs et permettra de les simplifier.
On déduit les Flux Théoriques de chaque étalon
par rapport à l’ étalon 1 en utilisant la réciproque
de la loi de Pogson :
| Magnitude catalogue | Flux théorique |
| Me1 | Fe1 = 1 |
| Me2 | Fe2 = Fe1 . 10 0.4 ( Me1 - Me2 ) = 10 0.4( Me1 - Me2 ) |
| Me3 | Fe3 = Fe1 . 10 0.4 ( Me1 - Me3 ) = 10 0.4( Me1 - Me3 ) |
| ...... | ......................................................................... |
| Men | Fen = Fe1 . 10 0.4 ( Me1 - Men ) = 10 0.4( Me1 - Men ) |
On en déduit le flux théorique de la SuperStar en ajoutant tous les flux :
![]()
On en déduit enfin la magnitude théorique de la SuperStar en utilisant la loi de Pogson :
Met = Me1-2,5.log ( Fet / Fe1 ) = Me1-2,5.log ( Fet )
Connaissant, la magnitude théorique de la Superstar Met, son flux mesuré Fet et le flux mesuré F2 de l'étoile, il est facile de calculer sa magnitude :
M2 = Met -2,5.log ( F2 / Fet )
3 ) Test de la méthode de la Superstar
Nous allons tester cette méthode sur deux exemples de tracer de courbes de lumière d'astérïodes. Dans le premier exemple, les étalons choisis seront bien plus brillants que l'astéroïde. Dans le deuxième, les magnitudes seront comparables.
Dans le premier test j'ai mesuré la magnitude de l'astéroïde
Amanda sur une série de 153 images prises le 25/12/98.
Parmi ces images, seules celles dont l'estimation de l'erreur de
magnitude
de Prism est inférieure à 0.15 ont été utilisées.
La SuperStar contient 5 étalons de magnitudes respectives :
10,19 11,3 12,14 10,82 et 11,12.
Les courbes obtenues par les deux méthodes sont présentés
sur le même graphe en vue de leur comparaison.
Voici le graphe de comparaison obtenu :
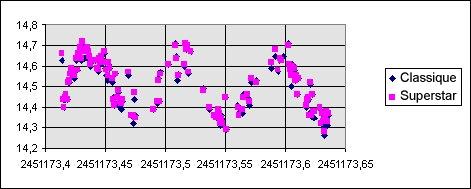
Et voici les erreurs de magnitude correspondantes:
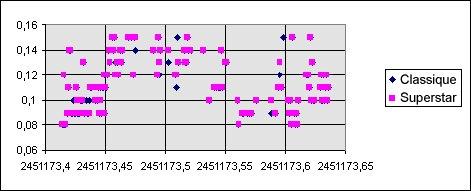
On ne constate aucune amélioration par rapport à la méthode avec un seul étalon !
Dans cet exemple, la méthode de la SuperStar n'apporte donc aucune
amélioration par rapport à un seul étalon. Pour améliorer
la mesure, il suffit plutôt de choisir parmi les étalons disponibles,
celui qui présente la plus petite erreur de mesure estimée
par Prism.
Cet echec est dû à la très grande différence
de luminosité entre les étalons et l'astéroïde.
Les étalons sont bien plus brillants. Ils présentent un écart
d'environs 4 magnitude ce qui représente un flux 40 fois plus fort.
Dans ces conditions, l'erreur de mesure vient presque uniquement de la
mesure du flux de l'astéroïde. Par conséquent, prendre
plusieurs étalons n'apporte aucune amélioration à
la mesure photométrique.
Pour le deuxième test, j'ai mesuré la magnitude de l'astéroïde
Monachia sur une série de 393 images prises le 30/12/99.
La SuperStar contient ici 3 étalons de magnitudes respectives
: 15,3 13,7 15,4.
Voici le graphe de comparaison obtenu :
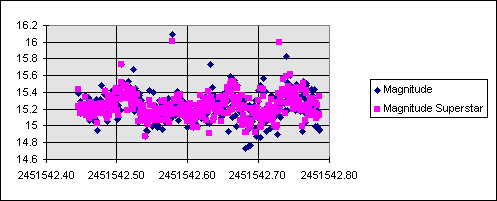
Et voici les erreurs de magnitude correspondantes:
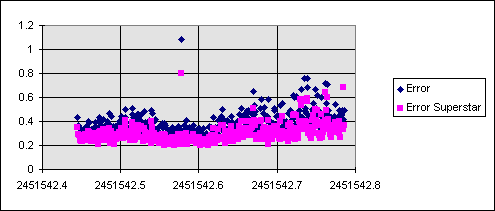
Cette fois ci l'amélioration est nettement visible particulièrement au niveau des erreurs de mesures.
Ces exemples montrent que la méthode de mesure photométrique
par Superstar n'est pas utile dans tous les cas. Elle ne servira que
lorsque
l'image ne contient que des étoiles de magnitude égale ou
inférieure à l'objet à analyser. Par contre si une
seule étoile bien plus brillante est disponible, il vaudra mieux
la prendre pour étalon à condition qu'elle ne soit pas variable.