
1 ) Introduction
Avec mes premières observations de Supernovae dans le cadre des
campagnes de l'association AUDE, j'ai commencé à m'intéresser
sérieusement aux problèmes de photométrie.
La principale fonction utilisée pour mesurer le flux des Supernovae
est la fonction de modélisation stellaire du PAP.
Je me suis immédiatement demandé quelle confiance pouvait-on
accorder à cette fonction et quelles pouvaient être ses limites
d'utilisation ?
Ne trouvant aucune documentation sur ce sujet, je me suis dit qu'il fallait absolument réaliser des tests de cette fonction.
Durant les vacances de Noël 1998, j'ai beaucoup travaillé
sur la photométrie et le tracé de courbes de lumière
d'astéroïdes.
Pour se faire, j'ai utilisé le puissant langage de programmation
script du PAP tout en l'améliorant encore.
Pendant ce travail, je me suis rendu compte que j'avais à ma
disposition pratiquement toutes les fonctions nécessaires aux tests
de la fonction de modélisation.
J'ai donc décidé de me lancer dans cette étude.
Je vous présente ici le compte rendu des premiers tests que j'ai pu réaliser.
2 ) Principe des tests
Des images sont créées grâce à la nouvelle
fonction script NewImage. Une étoile artificielle de profil gaussien
et de forme elliptique est créée dans ces images grâce
à la nouvelle fonction AddStar. On peux moduler tous les paramètres
de cette étoile : intensité maximum, largeur à mi-hauteur
suivant le petit et le grand axe de l'ellipse et angle du grand axe sur
l'horizontale. Une erreur est commise à cette étape car le
profil réel des étoiles n'est pas Gaussien.
Le flux réel de cette étoile artificielle est calculé
pendant sa création pour pouvoir le comparer par la suite au flux
mesuré. On connaît ainsi très précisément
le flux de cette étoile avant toute perturbation. On pourra donc
connaître précisément l'erreur de mesure de la fonction
de modélisation.
Du bruit gaussien peut être ajouté à l'image grâce à la fonction NoiseGauss. Seul le bruit du fond de ciel a été modélisé ici. Le bruit de photon de l'étoile artificielle n'a pas été simulé car il est négligeable pour les flux importants utilisés ici.
Voici le résultat de cette modélisation en ajoutant du
bruit :

La plupart des courbes qui suivent sont tracées en faisant varier un des paramètres de l'étoile synthétique et en comparant le flux mesuré par modélisation à sa valeur théorique. On peux ainsi analyser l'influence d'un paramètre sur la qualité de la modélisation et plus particulièrement sur la mesure du flux puisque nous nous intéressons surtout ici à la photométrie.
Les caractéristiques de l'image synthétique de base sont
les suivantes :
Intensité du fond de ciel : 1000 ADU
Intensité Maximum de l'étoile synthétique : 14000
ADU
Largeur à mi-hauteur de l'étoile synthétique :
2 pixels
Flux réel de l'étoile synthétique : 62196 ADU
La largeur de la fenêtre d'analyse de base est de 31 pixels
Avant de commencer les tests posons nous la question suivante :
A quelle erreur sur la magnitude correspond une erreur de 10 % sur
le flux d'une étoile ?
Prenons une étoile nous donnant un flux théorique de 100
ADU sur notre CCD. Supposons que les différentes perturbations de
la mesure nous donne une erreur de 10 % soit un flux de 90 ADU. On peux
alors calculer l'erreur de magnitude à :
Certains de mes propos exposés ici pourront peut être vous
sembler bien indulgents et vous penserez que j'accepte des erreurs de
mesure
bien importantes. Il vous faudra alors bien comprendre que je me place
ici du point de vue de l'amateur pour lequel une précision de 0.1
magnitude sur une étoile de magnitude 14 est tout à fait
acceptable. Cette précision permet par exemple de tracer des courbes
de lumière d'astéroïdes brillants tout à fait
exploitables.
Par contre l'amateur chevronné, plus exigeant, pourra trouver
des pistes pour améliorer ses mesures et surtout identifier les
paramètres les plus importants à affiner.
3 ) Influence du bruit de fond de ciel sur la mesure
du flux
Ce test doit permettre de vérifier l'influence du bruit du fond
de ciel présent dans l'image sur la qualité du Flux mesuré
donc sur la qualité de la mesure photométrique.
Pour un bruit gaussien donné, nous synthétisons 1000
images pour évaluer la dispersion des mesures en en mesurant l'écart
type.
Par exemple, pour un bruit ayant une dispersion de 15 ADU j'obtiens
le graphique :
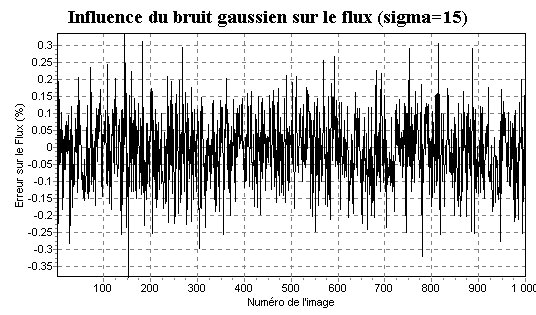
et un écart-type sur cette erreur de mesure du flux due au bruit de 0.098 %.
Pour un bruit double ayant une dispersion de 30 ADU j'obtiens le
graphique
:
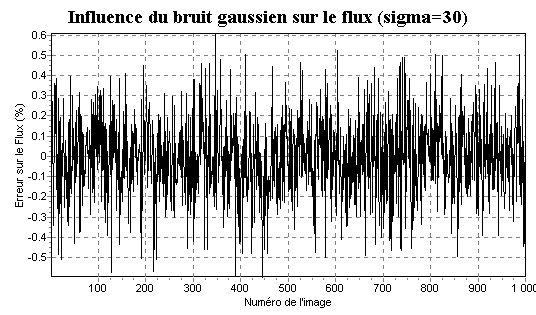
et un écart-type sur cette erreur de mesure du flux due au bruit de 0.21 % qui est bien doublé par rapport au test précédant.
En reprenant un bruit de 15 ADU d'écart-type, si l'on double
l'échantillonnage donc la focale, la largeur à mi-hauteur
de l'étoile est doublée et passe à 4 pixels. La surface
de l'étoile est multipliée par 4.
Par contre le flux de l'étoile artificielle reste le même.
Je mesure alors un écart-type de l'erreur de mesure du flux
de 0.47 %. Ce qui confirme qu'en augmentant la focale, on "dilue" le
signal
de l'étoile dans le bruit du fond de ciel et on dégrade la
mesure photométrique.
De ce chapitre, nous pouvons retenir que :
| Pour améliorer une mesure photométrique nous devons
: - Réduire la largeur à mi-hauteur des étoiles en diminuant la longueur focale, en soignant la mise au point et en prenant un télescope de diamètre plus grand. - Augmenter le flux reçu en augmentant le temps de pose et en augmentant le diamètre du télescope. - Réduire le bruit présent dans l'image en soignant les prétraitements et en observant dans un ciel le plus pur possible. |
4 ) Influence de la largeur à mi-hauteur des étoiles sur la mesure du Flux
Ce test doit permettre de vérifier l'influence de l'échantillonnage
d'une image sur la qualité du Flux mesuré donc sur la qualité
de la mesure photométrique.
L'erreur n'est due qu'à l'erreur de modélisation. Pour
ce test, j'ai fait varier la largeur à mi-hauteur de l'étoile
synthétique de 1 à 3 pixels
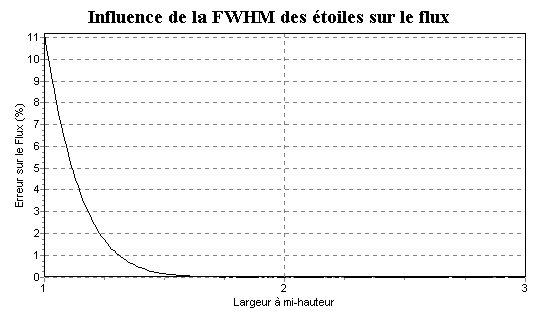
| On observe donc que dans l'absence d'autre perturbation que du bruit, la FWHM doit être supérieure à 1.5 pixels pour ne pas perturber la mesure et qu'à 1.25 pixels l'erreur est de 2 %. |
5 ) Influence d'un bougé sur le flux
Ici le phénomène de bougé est simulé en
déplaçant l'étoile dans l'image et en prenant les
valeurs maximum des pixels. Ceci peut être du à un défaut
de mise en station ou à un mauvais réglage de la vitesse
d'entraînement du télescope.
Le bougé simulé varie de 0 à 2 pixel :
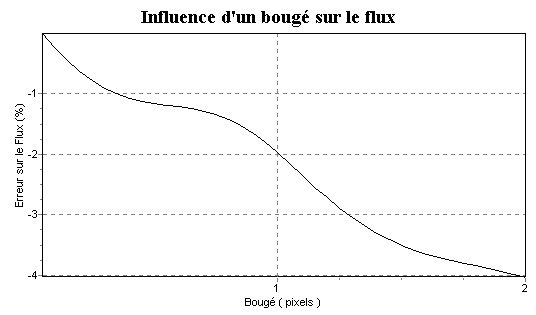
On peut constater que même pour un bougé important de 1
pixel, l'erreur de modélisation reste relativement faible. Il faut
néanmoins remarquer qu'ici nous ne tenons pas du tout compte de
l'effet d'étalement du flux de l'étoile dans le bruit du
fond de ciel.
| Il faut donc soigner la mise en station et la vitesse
d'entraînement
du télescope pour éviter tout effet de bougé. Mais on peux remarquer que l'algorithme de modélisation du PAP est donc assez peu sensible à l'effet de bougé. Si le bougé est inférieur à un pixel l'erreur reste inférieure à 2 %. |
6 ) Influence de la largeur de la fenêtre d'analyse sur le flux
Pour modéliser une étoile, le PAP découpe d'abord dans l'image un carré centré sur le pixel où l'utilisateur a cliqué. Ce n'est que dans un deuxième temps qu'il modélise l'étoile présente dans ce carré.
Ce test doit permettre de vérifier l'influence de la largeur
de la fenêtre d'analyse sur la qualité du Flux mesuré
donc sur la qualité de la mesure photométrique.
Dans le PAP cette largeur est réglée en modulant le paramètre
nommé 'demi-largeur de la fenêtre'.
Ce paramètre peut être choisi entre 3 et 15 pixels, ce
qui correspond à une largeur de la fenêtre d'analyse pouvant
varier de 7 à 31 pixels ( 2 fois la demi-largeur plus 1) .
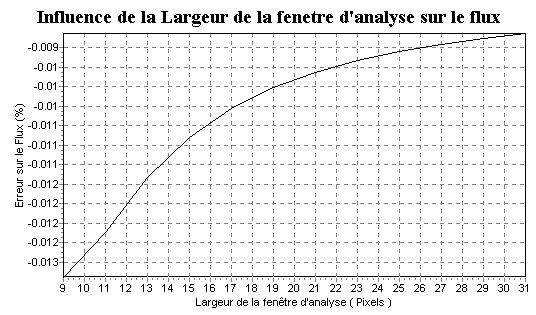
Nous constatons que pour une fenêtre de largeur minimale de 9
pixels, l'erreur de modélisation maximale est de 0.013 % ci qui
est négligeable.
| La largeur de la fenêtre d'analyse n'influe pas de façon significative sur la qualité des mesures photométriques par modélisation |
7 ) Influence d'une étoile proche sur la mesure
du flux
Ce test doit permettre de mesurer l'influence d'une étoile proche
sur la qualité de la modélisation.
Ce cas apparaît lorsqu'un astéroïde dont on veut
connaître la magnitude passe à côté d'une étoile.
Il n'est pas rare aussi qu'une Supernovae soit proche du noyau de sa
galaxie
hôte.
Il est alors important d'avoir une idée de l'influence de cette
étoile ou de ce noyau sur la mesure photométrique.
J'ai donc ajouté dans l'image à côté de l'étoile
à mesurer une autre étoile synthétique "parasite"
de même magnitude et de même forme.
Je l'ai placée d'abord en dehors de la fenêtre d'analyse
puis je l'ai rapprochée progressivement de la première étoile.
Avec une fenêtre d'analyse d'une demi-largeur de 15 pixels ( en
fait 15.5 pixels dans le PAP ) j'obtiens le graphe suivant :
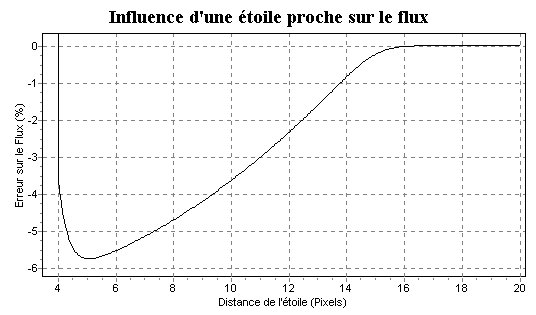
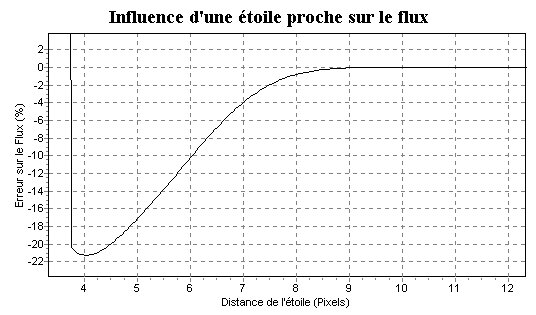
| Par conséquent pour une photométrie optimale, si l'on utilise une demi-largeur de la fenêtre d'analyse de L pixels, il faut veiller à ce qu'aucune étoile de largeur à mi-hauteur l ne soit à une distance plus faible que (L+0.5)-l de l'objet à mesurer. |
| Par conséquent il est impératif que l'objet soit séparé de l'étoile "parasite" par une distance supérieure à sa largeur à mi hauteur. |
| Par conséquent dans un champs riche en étoiles il faut mieux minimiser la taille de la fenêtre d'analyse. |
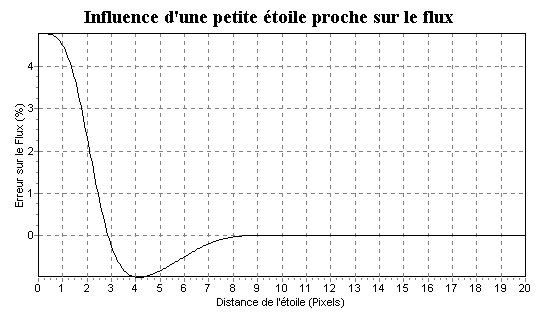
| Par conséquent l'influence, d'une étoile "parasite" bien moins lumineuse reste faible. |
8 ) Simulation d'un cas réel : l'astéroïde AMANDA
Après ces tests très théoriques, essayons de nous
rapprocher un peu plus de la réalité en simulant une mesure
réelle sur une image de l'astéroïde Amanda :

Étalon :
Coordonnée X = 485.1 pixels
Coordonnée Y = 174.51 pixels
FwhmX = 3.38 pixels
FwhmY = 2.69 pixels
Intensité maximum = 14300 ADU
Flux = 17242 ADU
Amanda :
Coordonnée X = 486.5 pixels
Coordonnée Y = 199.65 pixels
FwhmX = 3.19 pixels
FwhmY = 2.59 pixels
Intensité maximum = 340 ADU
Flux = 3409 ADU
Niveau du ciel : 164 ADU
Ecart-type du bruit : 11 ADU
Grâce à ces données, j'ai modélisé
au mieux Amanda et l'étalon et j'ai obtenu l'image synthétique
suivante :

Sur laquelle j'ai réalisé 1000 mesures de magnitudes en
recalculant le bruit à chaque image comme dans le chapitre 3.
Voici le résultat :
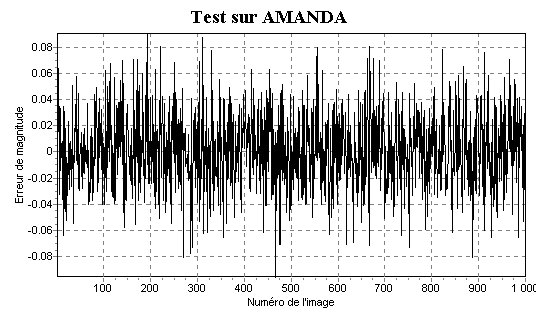
Nous mesurons un écart-type de l'erreur de mesure de 0.03 magnitudes
et une erreur maximum de 0.09 magnitudes.
Si l'on mesure la magnitude sur l'image réelle avec le PAP,
celui-ci nous donne une incertitude de 0.13 magnitudes. Ces deux
estimations
semblent bien correspondre. L'erreur mesurée par le PAP est plus
importante mais il fait bien voir que la simulation à ses limites.
En particulier l'erreur de suivi n'est pas forcément linéaire.
Il est donc normal qu'elle donne un résultat optimiste. Et n'oublions
que nous avons négligé le bruit des photons issus d'Amanda
dont le flux est relativement faible.
9 ) Conclusion
En conclusion, revoyons les enseignements tirés de chaque tests
:
Pour améliorer une mesure photométrique par modélisation
nous devons :
- Réduire la largeur à mi-hauteur des étoiles
en diminuant la longueur focale, en soignant la mise au point et en
prenant
un télescope de diamètre plus grand.
- Augmenter le flux reçu en augmentant le temps de pose et
en augmentant le diamètre du télescope.
- Réduire le bruit présent dans l'image en soignant
les prétraitements et en observant dans un ciel le plus pur possible.
- Avoir une largeur à mi-hauteur des étoiles supérieure
à 1.5 pixels.
- Soigner la mise en station et la vitesse d'entraînement
du télescope pour éviter tout effet de bougé. Mais
un bougé inférieur à un pixel reste acceptable.
- Si l'on utilise une demi-largeur de la fenêtre d'analyse
de L pixels, il faut veiller à ce qu'aucune étoile de largeur
à mi-hauteur l ne soit à une distance plus faible que (L+0.5)-l
de l'objet à mesurer.
- Il est impératif que l'objet soit séparé
de l'étoile "parasite" par une distance supérieure à
sa largeur à mi hauteur.
Dans un article suivant, je ferai à nouveau les tests que nous
venons de voir ici, mais en utilisant une fonction de photométrie
d'ouverture circulaire.
J'espère ainsi pouvoir mettre en évidence les inconvénients
et les avantages de chacune des deux méthodes.