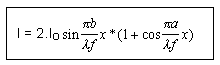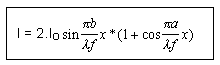Mesure
de la distance angulaire entre
étoiles
doubles par interférométrie
PRINCIPE de la METHODE
L'onde lumineuse , en provenance d'une source ponctuelle (étoile)
passant à travers 2 fentes donne au delà des fentes des franges
d'interférence constituées de :
- points brillants lieu où les ondes issues des 2 fentes arrivent
en phase (les amplitudes des ondes s'ajoutent de façon constructive)
.
- points sombres lieu où les ondes arrivent en opposition de
phase(les
ondes sont destructives) .
On rappelle que pour pouvoir observer des franges d'interférence
il faut que les 2 sources secondaires soient cohérentes (même
fréquence) et synchrones (même phase) . Le dispositif imaginé
par Thomas YOUNG (médecin /1773-1829) proposé en 1801 permet
à partir d'une seule source de diviser le front d'onde et d'obtenir
à la sortie des fentes 2 sources (secondaires) nécessairement
cohérentes et synchrones.
Dans le cas où la source est double ( Etoiles doubles) les 2
figures d'interférences se superposent . L'examen théorique
et pratique de cette superposition permet d'en déduire la distance
angulaire d (") entre les 2 sources . Et dans le cas de 2 doubles
réelles
(en rotation autour d'un centre de gravité commun) , il est possible
de suivre l'évolution de la distance angulaire entre les 2 étoiles
.
On rappelle qu'au phénomène d'interférence (superposition
de 2 ondes) se superpose le phénomène de diffraction (déformation
du front d'onde par un obstacle (fente) . La diffraction à pour
conséquence une modulation de l'amplitude de l'onde résultante
.
UN PEU DE THEORIE :
On montre que l'intensité résultant de la superposition
de 2 ondes est donnée par la relation :
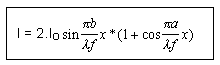
Notations:
a = distance entre les 2 fentes (axe à axe)
b = largeur des fentes
f = distance focale de la lentille de projection
Lambda = longueur d'onde de la radiation
x = coordonnée du point sur l'écran de projection
d = distance angulaire entre les 2 sources (étoiles)
i = interfrange (distance entre 2 maxima successifs)
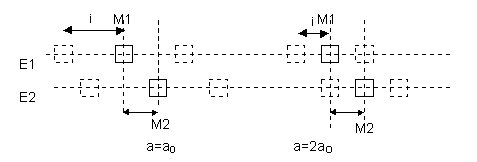
M1M2 = Cte = distance entre les 2 maxima d'interférence pour
un même couple stellaire (E1,E2) , donc pour une même distance
angulaire d"
Seul l'interfrange i , dépend de la distance a entre les 2 sources
Cette équation justifie le fait que x variant sur le plan ,
I passe par des maxima (principal et secondaires) et ce pour chaque
système
propre à une étoile .
Ainsi en faisant varier la distance a entre les 2 fentes , on va
observer
des chevauchements et des brouillages des 2 systèmes de franges
.
On montre que les 2 systèmes vont s'interpénétrer
(brouillage) , c'est à dire le maximum d'un des système correspond
au minimum de l'autre quand la distance angulaire ? entre les 2 étoiles
obéit à la relation :
1 rad=206.265"
Le principe de l'expérience consiste donc à faire varier
, en partant de la valeur la plus faible possible , la distance a entre
les 2 fentes jusqu'à ce que l'on observe le 1° brouillage des
2 systèmes d'interférence . Alors a = a0
- On pourra vérifier que si l'on double cette valeur a= a0
correspondant
au 1° brouillage , on obtient un chevauchement des 2 systèmes
d'interférence .
(donc pour a=2a0)
- Pour a=3a0 , on vérifiera aussi que l'on obtient un 2°
brouillage , moins net du fait des phénomènes de diffraction
qui interviennent sur l'amplitude de l'onde résultante .
UN PEU DE BRICOLAGE :
On confectionnera un capuchon destiné à être positionné
devant le télescope (C8) .
Il permettra de placer devant la lame de fermeture :
- soient 2 fentes de largeur b= 1cm et dont l'entre axe a sera
soit
réglable
soit déterminé et taillé pour une seule valeur . Il
faudra disposer d'autant de caches qu'il y aura de largeur de fentes à
tester !!!
- soit un réseau de fentes dont le pas sera égal à a
. La luminosité du montage en sera nettement améliorée
.
En réalité ,
pour les tests nous avons opéré à l'envers afin
de vérifier le bon fonctionnement du montage .
- Connaissant la distance angulaire d"=7,9" , de 2 étoiles (Gamma
Ari ) nous en avons déduit la distance a=8mm à donner à
notre cache pour qu'il y ait un système qui s'interpénètre
pour la 1° fois .
- En doublant cette distance (a=16mm) nous avons construit un 2°
cache
qui devait fournir un système d'interférences qui se chevauchaient
.
- Et en triplant , (a=24mm) nous devions avoir un cache qui nous
permettait
de retrouver un système d'interférences intercalé
à nouveau .
Il suffit ensuite de trouver un autre couple intéressant et travailler
en cherchant à déterminer d" à partir de fentes dont
on fait varier l'entre-axe a
Cas de Alpha Gem (Castor) m= 2,0/2,9 - d''=2,7"
IMPORTANT !
Pour avoir des systèmes d'interférences de même
intensité , il faudra choisir des couples ayant sensiblement la
même magnitude apparente m . Dans le cas contraire le chevauchement
ou l'interpénétration des figures d'interférences
seront difficiles à mettre en évidence .
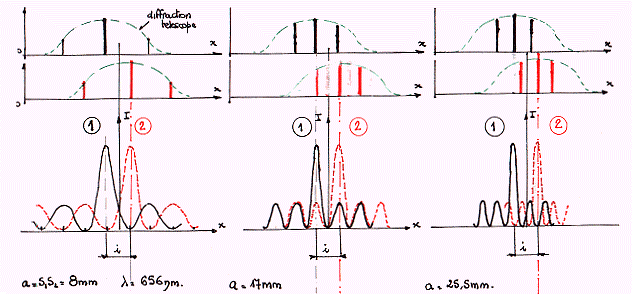
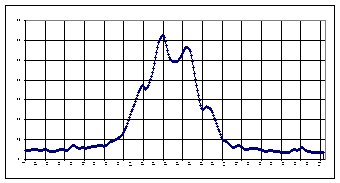
On observera :
- la distance entre 2 maxima reste bien constante pour un même
système
double
- seul l'interfrange i varie en fonction de a ( quand on
augmente a, i
diminue)
- la tâche la plus brillante représente le maximum central .
- les autres maxima sont atténués par le phénomène
de diffraction propre à chaque fente . Ce phénomène
rend délicat l'identification d'un maximum relatif à une
étoile et d'un autre maximum relatif à l'autre étoile
. Il faut être vigilant !
|
Distance entre fentes a (mm) |
Longueur d'onde (µm) |
Distance Angulaire ('' arc) |
| Essai n°1 |
8 |
0.65 |
8.34 (1° interpénétration) |
| Cas Théorique |
8.5 |
0.65 |
7.9 |
| Essai n°2 |
10.7 |
0.65 |
1° chevauchement |
| Essai n°3 |
25.5 |
0.65 |
2° interpénétration |
Autres exemples de travaux


Etalonnage des focales à partir du C8 (F=2000 mm) sur un triplet

ANALYSE
PHOTOMETRIQUE
DES FIGURES D'INTERFERENCES
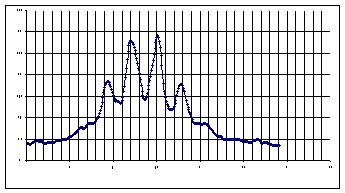
EXEMPLE N°1 : g
Ari – m1=4,7/m2=4,8- r
=7,9’’ (6 Janvier 1998)
Télescope C8 + Doubleur (F=4670mm)
+ Filtre rouge (0.65µm)
Caméra Hisis22 Binning 2*2 Pose 2s
Observatoire de Narbonne – Atelier Science
- Lycée Diderot .
2 Fentes a=8mm 1ere interpénétration

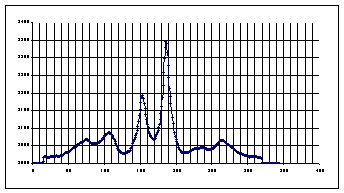
2 Fentes a=17mm 1er chevauchement

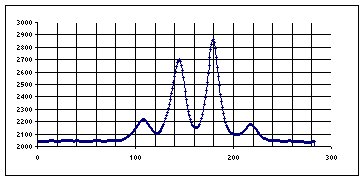
2 Fentes a=25.5mm 2eme interpénétration

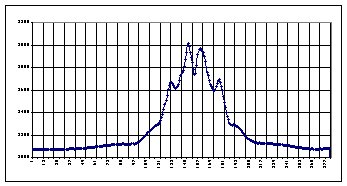
EXEMPLE N°2 : a
Gem (Castor) m1=2,0/m2=2,9 r
’’=2,7’’ (18 Février 1998)
Télescope C8 + Doubleur (F=4670mm)
+ Filtre rouge (0.65µm)
Caméra Hisis22 Binning 2*2 Pose 5s
Observatoire de Narbonne – Atelier Science
- Lycée Diderot .
2 Fentes a= 25mm 1ere interpénétration

EXEMPLE N°3 : 52 Ori – m1=6,0 /m2=6,1
- r
’’=1,4’’
(18 Février 1998)
Télescope C8 + Doubleur (F=4670mm)
+ Filtre rouge (0.65µm)
Caméra Hisis22 Binning 2*2 Pose 10s
Observatoire de Narbonne – Atelier Science
- Lycée Diderot .
2 fentes de a=48mm